Elongation

Increasing size of a power plant is generally accompanied by a decrease in specific costs; the costs per unit output drop, and the amortization period shortens.
This is particularly true in this case, because of the weightlessness of the decisive converter component, the floating lifting body. While, for example, the infrastructure costs of a wind-powered generator - foundation, installation, connection to grid - of 30% of capital costs, on average, for a rotor diameter of 15 metres sink to 15% for 30 metres (U.S. figures), in the proposed hydroelectric plant, the decrease covers not only items such as the concrete structures, but even the generator itself, because of the only minor increase in daywork.
The output P of the oscillating lifting body is a linear growth function of its area, and thus of its length at constant width. For an identical speed of flow v, the Joukowski formula for the output can be transformed into the equation of condition for the lifting-body length, l:

l = P/C
where C = c_a × v² × p/2 × h × s/t × η can be regarded as a constant.

For the economy of scale:

Costs K ∼ output P^α with α<1

K_s = K/P ∼ P^α-1

The generating costs in cents per kilowatt-hour, for roughly equal operating costs, are represented by such a graph:

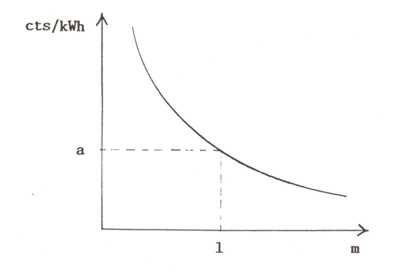
For any desired kilowatt-hour generating price a (cents/kWh), a respective lifting-body length l_a

Lutz Kroeber 2007